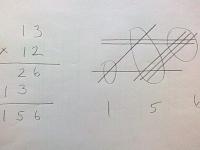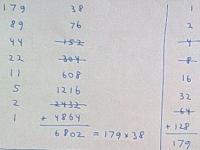Notes (Notlar)
Türkçe'deki notlarım aşağıdadır (my notes in Turkish are below).
The word notes
here refers to course lecture notes or other
so-called expository writing. I may blame my calculus teacher (about
whom I wrote a blog
article) for first giving me the idea that the best teachers create
their own textbooks. I do not necessarily agree with this any more, at
least not in all cases; but the fact remains that, in teaching a course,
I am usually not satisfied to follow anybody's textbook but my own.
Expository
writing may be based on historical
research. It is possible that mathematical research—the
discovery of new theorems—may result; I cite my paper, Model-theory of vector-spaces over
unspecified fields,
as an example. I have also drafted a monograph on Euclid's number theory,
arguing for a (more or less) new and (I think) better way of
understanding this theory.
In English (İngilizce’de)
Course notes
Algebra
- Finite Fields 2017 | 2016 (for a course at the Nesin Mathematics Village)
- Linear algebra notes (in html, for an undergraduate course, original in 2000)
- Groups and Rings, for a first-year graduate course.
Geometry
Conic Sections
(31 pages, size A5, March 21, 2015): for use in a course of analytic geometry- See also my courses in projective and hyperbolic geometry (based on Pappus and Lobachevski):
Logic
Logical Paradoxes
(8 pages, size A5, September 23, 2013)- Foundations of Mathematical Practice (236 pages, size A5, September 24, 2010), for a first-year undergraduate course.
- Minimalist Set Theory (166+ pages, 2011), for a third-year undergraduate course.
- Recursion and Induction: Notes on Mathematical Logic and Model Theory (109 pages, size A4, September 17, 2008), for a fourth-year undergraduate course.
- Ultraproducts and nonstandard analysis (notes from several courses in Şirince)
Number theory
- Elementary Number Theory (196 pages), originally for a third-year undergraduate course.
- Elementary Number Theory II, given at METU in 2008 (153 pages, size A5, 12 point type, revised January 5, 2018)
History
Other
Logic
Ordinal Analysis
(48 pages, size A5, 12 point type, May 29, 2018): This is a philosophy of mathematics and the teaching of it, originating as a preface in English to the Turkish set-theory text listed below.- Undecidability of C(T0,
T1) (version of April 4, 2017; 14 pages, size
A5):
The text is based on work of Kim and Roush and formed part of my 1997 doctoral thesis, which otherwise produced Function fields and elementary equivalence
- Topics related to the Compactness Theorem
Descartes as Model Theorist
- Istanbul Model Theory Seminar
- Morley's Categoricity Theorem
- Ultraproducts
Geometry
- “Thales of Miletus: Sources and Interpretations” (over a hundred pages of notes, prepared originally for the talk “Thales Kanıt kavramının öncüsü olarak,” September 24, 2016, listed below
- Analytic Geometry, including
Thales and the Nine-point Conic
(published in the De Morgan Gazette)Conic Sections
(as also above)Abscissas and Ordinates
(now published in the Journal of Humanistic Mathematics)Analytic Geometry
(part of which becameAbscissas and Ordinates
)
- Geometry, including
Commensurability and Symmetry
(now published asOn Commensurability and Symmetry
in the Journal of Humanistic MathematicsFrom Euclid to Descartes
Çarpma yöntemleri (Facebook'a koyduğum resimler) // Multiplication methods (pictures I put on Facebook)
Türkçede (in Turkish)
- Platonik Cisimler (Platonic Solids)
- Arşimet Cisimleri (Archimedean solids)
- Thales Kanıt kavramının öncüsü olarak (24 Eylül 2016 konuşma)
- Sonsuzküçük Analiz
- Matematik Paradoksları
- Koni kesitleri (conic sections)
- [Aksiyomatik] Kümeler kuramı (axiomatic set theory)
- Lineer Cebir
- Modeller kuramı (model theory)
- Önermeler mantığı (propositional logic)
- Posterler (posters)